
Practical considerations, such as not being able to read.Ethical considerations, such as being a minor or being unable to give informed consent.In other words, individuals who meet the inclusion criteria may also possess additional characteristics that can interfere with the outcome of the study. These can also include those that lead to participants withdrawing from a research study after being initially included. Control variables: Fitness level, tobacco use, medications usedįailure to properly define inclusion and exclusion criteria can undermine your confidence that causal relationships exist between treatment and control groups, affecting the internal validity of your study and the generalizability ( external validity) of your findings.Įxclusion criteria comprise characteristics used to identify potential research participants who should not be included in a study.Study-specific variables: Type and stage of disease, previous treatment history, presence of chronic conditions, ability to attend follow-up study appointments, technological requirements (e.g., internet access).Demographic characteristics: Age, gender identity, ethnicity.Examples of common inclusion and exclusion criteria are: This allows researchers to study the needs of a relatively homogeneous group (e.g., people with liver disease) with precision. Collectively, they’re known as eligibility criteria, and establishing them is critical when seeking study participants for clinical trials. Inclusion and exclusion criteria determine which members of the target population can or can’t participate in a research study.
INCLUSION EXCLUSION PRINCIPLE FOR FREE
Try for free Inclusion and Exclusion Criteria | Examples & Definition non-probability samplingĮliminate grammar errors and improve your writing with our free AI-powered grammar checker. We will denote by $X$ the set of permutations in which the first element is $\leq 1$ and $Y$ the set of permutations in which the last element is $\geq 8$. Let's count the number of "bad" permutations, that is, permutations in which the first element is $\leq 1$ and/or the last is $\geq 8$. Task: count how many permutations of numbers from $0$ to $9$ exist such that the first element is greater than $1$ and the last one is less than $8$. Tasks asking to "find the number of ways" are worth of note, as they sometimes lead to polynomial solutions, not necessarily exponential. The inclusion-exclusion principle is hard to understand without studying its applications.įirst, we will look at three simplest tasks "at paper", illustrating applications of the principle, and then consider more practical problems which are difficult to solve without inclusion-exclusion principle. The Stern-Brocot Tree and Farey Sequences Tortoise and Hare Algorithm (Linked List cycle detection)ġ5 Puzzle Game: Existence Of The Solution Optimal schedule of jobs given their deadlines and durations MEX task (Minimal Excluded element in an array) Search the subsegment with the maximum/minimum sum RMQ task (Range Minimum Query - the smallest element in an interval) Kuhn's Algorithm - Maximum Bipartite Matching Maximum flow - Push-relabel algorithm improved Maximum flow - Ford-Fulkerson and Edmonds-Karp Lowest Common Ancestor - Tarjan's off-line algorithm Lowest Common Ancestor - Farach-Colton and Bender algorithm Second best Minimum Spanning Tree - Using Kruskal and Lowest Common AncestorĬhecking a graph for acyclicity and finding a cycle in O(M) Minimum Spanning Tree - Kruskal with Disjoint Set Union Number of paths of fixed length / Shortest paths of fixed length Strongly Connected Components and Condensation Graphĭijkstra - finding shortest paths from given vertexīellman-Ford - finding shortest paths with negative weightsįloyd-Warshall - finding all shortest paths Half-plane intersection - S&I Algorithm in O(N log N)Ĭonnected components, bridges, articulations points Search for a pair of intersecting segmentsĭelaunay triangulation and Voronoi diagram


Pick's Theorem - area of lattice polygons
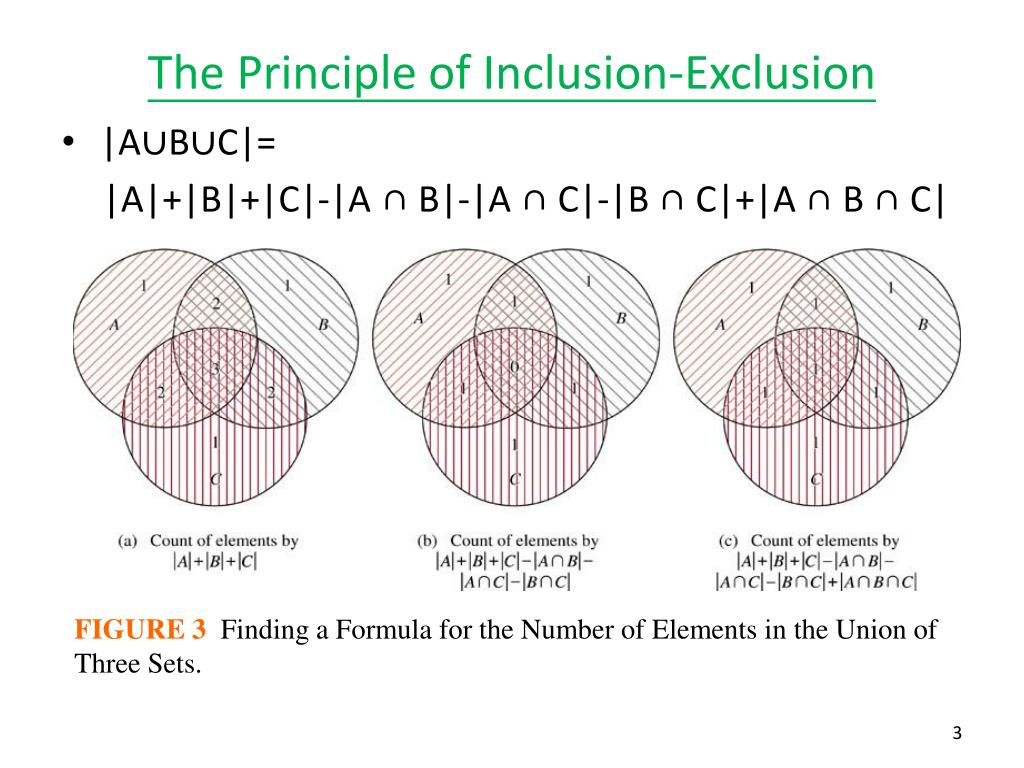
The number of permutations without fixed points (derangements)īurnside's lemma / Pólya enumeration theoremįinding the equation of a line for a segmentĬheck if points belong to the convex polygon in O(log N) The number of ways of going from a cell to another The number of strings that satisfy a given pattern The number of integers in a given interval which are multiple of at least one of the given numbers The number of relative primes in a given interval Generalization for calculating number of elements in exactly r sets The formulation in terms of probability theory Manacher's Algorithm - Finding all sub-palindromes in O(N) Euclidean algorithm for computing the greatest common divisorĭeleting from a data structure in O(T(n) log n)ĭynamic Programming on Broken Profile.


 0 kommentar(er)
0 kommentar(er)
